Large language models (LLMs) are rapidly advancing, showing impressive capabilities in many areas, including complex mathematical reasoning. From generating code to tackling intricate equations, these AI systems are becoming increasingly sophisticated. However, despite their apparent prowess, a critical question remains: do LLMs genuinely understand the underlying mathematical principles, or are they simply adept at recognizing and mimicking patterns? This question is particularly crucial for applications in advanced science and technology, where university-level symbolic mathematics – like integration, limits, and differential equations – is a fundamental requirement.
Traditional benchmarks designed to assess LLMs’ mathematical abilities often fall short in evaluating their core symbolic manipulation skills. Many existing tests focus on pre-university level arithmetic or rely on multiple-choice questions, which don’t truly capture the open-ended nature of real-world problem-solving. Furthermore, word-problem benchmarks often conflate text understanding with mathematical ability, making it difficult to isolate and assess pure symbolic reasoning.

We introduce ASyMOB: Algebraic Symbolic Mathematical Operations Benchmark, an assessment framework specifically designed to evaluate LLMs’ capabilities in symbolic manipulation. What makes ASyMOB unique is its focused scope, targeting only pure symbolic math problems without any extraneous textual or graphical information. It features a massive dataset of 17,092 unique math challenges, systematically organized by similarity and complexity. A key innovation of ASyMOB is its use of “perturbations” – small numerical or symbolic changes introduced to original “seed” problems. This allows researchers to analyze how LLMs’ performance degrades under these controlled variations, providing insights into their generalization capabilities and potential reliance on memorized patterns.

The results from evaluating leading LLMs on ASyMOB show substantial degradation in performance when models face perturbed versions of the questions, with success rates dropping considerably (up to -70% in certain perturbation categories) compared to the unperturbed set. This suggests that many LLMs rely on memorized patterns rather than a deep understanding of symbolic math. However, the most advanced models (o4-mini and Gemini 2.5 Flash) demonstrate not only high baseline performance, but also remarkable robustness against perturbations, exhibiting much less performance degradation than their counterparts.
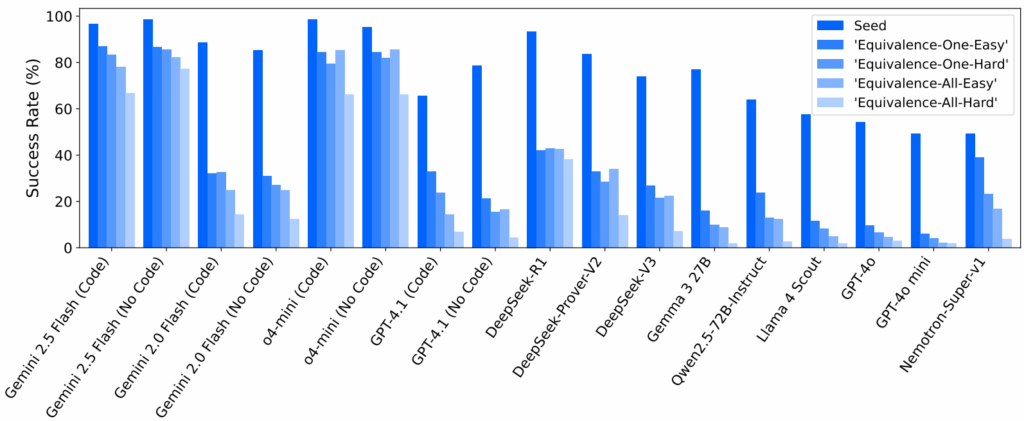
ASyMOB tests models both with and without use of code interpreters. While weaker models sometimes see substantial boosts when allowed to run Python internally (sometimes improving by more than 30% on perturbed problems), frontier models show only marginal gains. This resilience to perturbations in frontier LLMs, with and without code execution, hints at a potential “phase transition” in their generalization capabilities, suggesting they may be moving beyond simple memorization towards a more genuine mathematical understanding.
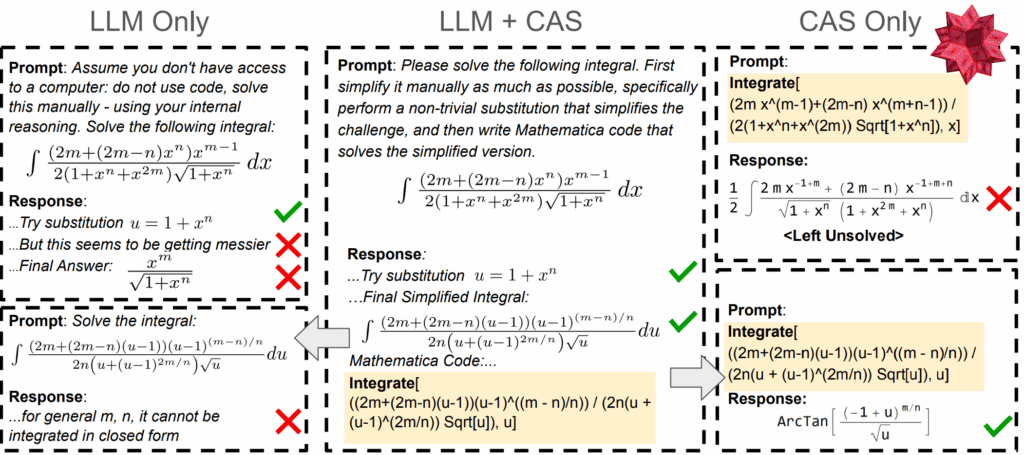
Perhaps most intriguingly, ASyMOB highlights cases where neither pure LLMs nor traditional computer algebra systems (CAS) like SymPy or Mathematica can solve certain integrals, but a hybrid approach combining LLM-guided simplification with CAS execution succeeds. This finding underscores the complementary strengths of human-like strategic reasoning and machine-exact symbolic manipulation – pointing toward a future where LLMs and CAS co-evolve for even more powerful mathematical problem-solving.
Overall, the ASyMOB benchmark quantifies current limitations in symbolic math reasoning and charts a path forward. By revealing how small perturbations can derail models that seemed otherwise competent, it challenges researchers to develop training and prompting techniques that foster true generalization rather than rote pattern matching. The stark contrast between models that collapse under perturbations and the handful of frontier systems that maintain strong accuracy suggests we are on the cusp of a new era, raising new questions: Which mathematical tasks will continue to challenge LLMs? Which tools will prove the most valuable? How will it change the role of the mathematician in the process of discovery?
For more details, you can refer to the full paper. The project repository is available on GitHub: ASyMOB code repository, and the ASyMOB dataset is available on Hugging Face: ASyMOB data.